Vibrații armonice
Grafice de funcții f(X) = păcat( X) și g(X) = cos( X) pe planul cartezian.
oscilație armonică- fluctuații în care o mărime fizică (sau orice alta) se modifică în timp conform unei legi sinusoidale sau cosinusului. Ecuația cinematică a oscilațiilor armonice are forma
,Unde X- deplasarea (abaterea) punctului oscilant de la pozitia de echilibru la momentul t; A- amplitudinea oscilaţiei, aceasta este valoarea care determină abaterea maximă a punctului de oscilaţie de la poziţia de echilibru; ω - frecvența ciclică, o valoare care arată numărul de oscilații complete care au loc în 2π secunde - faza completă a oscilațiilor, - faza inițială a oscilațiilor.
Oscilatie armonica generalizata in forma diferentiala
(Orice soluție netrivială a acestei ecuații diferențiale este o oscilație armonică cu o frecvență ciclică)
Tipuri de vibrații
Evoluția în timp a deplasării, vitezei și accelerației în mișcare armonică
- Vibrații libere sunt realizate sub acţiunea forţelor interne ale sistemului după ce sistemul a fost scos din echilibru. Pentru ca oscilațiile libere să fie armonice, este necesar ca sistemul oscilator să fie liniar (descris prin ecuații liniare ale mișcării) și să nu existe disipare a energiei în el (acesta din urmă ar provoca amortizare).
- Vibrații forțate efectuată sub influența unei forțe periodice externe. Pentru ca acestea să fie armonice, este suficient ca sistemul oscilator să fie liniar (descris prin ecuații liniare ale mișcării), iar forța externă însăși se schimbă în timp ca o oscilație armonică (adică dependența de timp a acestei forțe să fie sinusoidală) .
Aplicație
Vibrațiile armonice se disting de toate celelalte tipuri de vibrații din următoarele motive:
Vezi si
Note
Literatură
- Fizică. Manual elementar de fizică / Ed. G. S. Lansberg. - Ed. a 3-a. - M ., 1962. - T. 3.
- Khaykin S. E. Bazele fizice ale mecanicii. - M., 1963.
- A. M. Afonin. Bazele fizice ale mecanicii. - Ed. MSTU im. Bauman, 2006.
- Gorelik G.S. Vibrații și valuri. Introducere în acustică, radiofizică și optică. - M .: Fizmatlit, 1959. - 572 p.
Fundația Wikimedia. 2010 .
- Comuna Malbork
- popoare din Africa
Vedeți ce sunt „Vibrațiile armonice” în alte dicționare:
OSCILAȚII ARMONICE Enciclopedia modernă
Vibrații armonice- OSCILAȚII ARMONICE, modificări periodice ale unei mărimi fizice care apar conform legii sinusului. Grafic, oscilațiile armonice sunt reprezentate printr-o curbă sinusoidală. Oscilațiile armonice sunt cel mai simplu tip de mișcare periodică, caracterizată prin... Dicţionar Enciclopedic Ilustrat
Vibrații armonice- Fluctuaţii în care o mărime fizică se modifică în timp conform legii sinusului sau cosinusului. Grafic G. to. sunt reprezentate printr-o curbă sinusoidală sau cosinus (vezi fig.); ele pot fi scrise sub forma: x = Asin (ωt + φ) sau x ... Marea Enciclopedie Sovietică
OSCILAȚII ARMONICE- OSCILAȚII ARMONICE, mișcare periodică precum mișcarea unui PENDUL, oscilații atomice sau oscilații într-un circuit electric. Un corp efectuează oscilații armonice neamortizate atunci când oscilează de-a lungul unei linii, mișcându-se la fel... ... Dicționar enciclopedic științific și tehnic
OSCILAȚII ARMONICE- fluctuații, la care ryh fizic. (sau orice altă valoare) se modifică în timp conform unei legi sinusoidale: x=Asin(wt+j), unde x este valoarea valorii oscilante din data. moment de timp t (pentru G. mecanică la., de exemplu, deplasare sau viteză, pentru ... ... Enciclopedia fizică
vibratii armonice- Vibrații mecanice, în care coordonatele generalizate și (sau) viteza generalizată se modifică proporțional cu sinusul cu un argument dependent liniar de timp. [Culegere de termeni recomandați. Problema 106. Vibrații mecanice. Academia de Științe... Manualul Traducătorului Tehnic
OSCILAȚII ARMONICE- fluctuații, la care ryh fizic. (sau orice altă) mărime se modifică în timp conform unei legi sinusoidale, unde x este valoarea mărimii oscilante la momentul t (pentru G. mecanică la., de exemplu, deplasarea și viteza, pentru tensiunea și curentul electric) .. . Enciclopedia fizică
OSCILAȚII ARMONICE- (vezi), în care fizic. valoarea se modifică în timp, conform legii sinusului sau cosinusului (de exemplu, modificări (vezi) și viteza în timpul oscilației (vezi) sau modificări (vezi) și puterea curentului cu G. electrică la.) ... Marea Enciclopedie Politehnică
OSCILAȚII ARMONICE- se caracterizează printr-o modificare a valorii oscilante x (de exemplu, abaterea pendulului de la poziția de echilibru, tensiunea în circuitul de curent alternativ etc.) în timpul t conform legii: x = Asin (?t + ?), unde A este amplitudinea oscilațiilor armonice, ? colt…… Dicţionar enciclopedic mare
Vibrații armonice- 19. Oscilații armonice Oscilații în care valorile mărimii oscilante se modifică în timp conform legii Sursa... Dicționar-carte de referință de termeni ai documentației normative și tehnice
OSCILAȚII ARMONICE- periodic fluctuații, cu schimbarea krykh în timp fizic. magnitudinea apare conform legii sinusului sau cosinusului (vezi fig.): s = Asin (wt + f0), unde s este abaterea valorii fluctuante de la cf. valoare (de echilibru), A=amplitudine constantă, w= circulară constantă... Marele dicționar politehnic enciclopedic
Oscilații care apar sub acțiunea forțelor externe, care se schimbă periodic (cu o furnizare periodică de energie din exterior către sistemul oscilator)
Transformarea energiei
Pendul de primăvară
![]()
Frecvența ciclică și, respectiv, perioada de oscilație sunt:
![]()
 Un punct material atașat de un arc perfect elastic
Un punct material atașat de un arc perfect elastic
Ø diagramă a energiei potențiale și cinetice a unui pendul cu arc pe coordonata x.
Ø grafice calitative ale dependențelor energiei cinetice și potențiale în timp.





Ø Forţat
Ø Frecvența oscilațiilor forțate este egală cu frecvența modificărilor forței externe
Ø Dacă Fbc se modifică conform legii sinusului sau cosinusului, atunci oscilațiile forțate vor fi armonice

Ø Cu auto-oscilatii este necesara o alimentare periodica de energie din sursa proprie in interiorul sistemului oscilator
Oscilațiile armonice sunt oscilații în care valoarea oscilantei se modifică în timp conform legii sinusului sau cosinusului

ecuaţiile oscilaţiilor armonice (legile mişcării punctelor) au forma


Vibrații armonice
se numesc astfel de oscilații, în care valoarea oscilantei variază în timp conform legiisinusului
saucosinus
.
Ecuația vibrațiilor armonice se pare ca:
,
unde un - amplitudinea oscilației
(valoarea celei mai mari abateri a sistemului de la poziția de echilibru); -frecvență circulară (ciclică).
Argumentul cosinus se schimbă periodic - numit faza de oscilatie
. Faza de oscilaţie determină deplasarea mărimii oscilante din poziţia de echilibru la un moment dat t. Constanta φ este valoarea fazei la momentul t = 0 și se numește faza iniţială a oscilaţiei
. Valoarea fazei inițiale este determinată de alegerea punctului de referință. Valoarea x poate lua valori cuprinse între -A și +A.
Intervalul de timp T, după care se repetă anumite stări ale sistemului oscilator, numită perioadă de oscilație
. Cosinusul este o funcție periodică cu o perioadă de 2π, prin urmare, pe o perioadă de timp T, după care faza de oscilație va primi un increment egal cu 2π, starea sistemului care efectuează oscilații armonice se va repeta. Această perioadă de timp T se numește perioada oscilațiilor armonice.
Perioada oscilaţiilor armonice este
: T = 2π/.
Se numește numărul de oscilații pe unitatea de timp frecvența de oscilație
ν.
Frecvența vibrațiilor armonice
este egal cu: ν = 1/T. Unitate de frecvență hertz(Hz) - o oscilație pe secundă.
Frecvența circulară = 2π/T = 2πν oferă numărul de oscilații în 2π secunde.
Oscilatie armonica generalizata in forma diferentiala
![]()
Grafic, oscilațiile armonice pot fi descrise ca o dependență a lui x de t (Fig. 1.1.A) și metoda amplitudinii rotative (metoda diagramei vectoriale)(Fig.1.1.B) .
Metoda amplitudinii rotative vă permite să vizualizați toți parametrii incluși în ecuația oscilațiilor armonice. Într-adevăr, dacă vectorul amplitudine A situată la un unghi φ față de axa x (vezi Figura 1.1. B), atunci proiecția sa pe axa x va fi egală cu: x = Acos(φ). Unghiul φ este faza inițială. Dacă vectorul A pus în rotație cu o viteză unghiulară egală cu frecvența circulară a oscilațiilor, apoi proiecția capătului vectorului se va deplasa de-a lungul axei x și va lua valori cuprinse între -A și +A, iar coordonatele acestei proiecții se va modifica în timp conform legii:
.
Astfel, lungimea vectorului este egală cu amplitudinea oscilației armonice, direcția vectorului în momentul inițial formează un unghi cu axa x egal cu faza inițială a oscilației φ, iar modificarea unghiului de direcție. cu timpul este egală cu faza oscilaţiilor armonice. Timpul pentru care vectorul amplitudine face o rotație completă este egal cu perioada T a oscilațiilor armonice. Numărul de rotații ale vectorului pe secundă este egal cu frecvența de oscilație ν.
Cel mai simplu tip de vibrații sunt vibratii armonice- fluctuatii in care deplasarea punctului oscilant fata de pozitia de echilibru se modifica in timp dupa legea sinusului sau cosinusului.
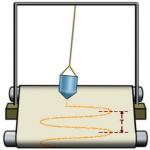
Deci, cu o rotire uniformă a mingii în jurul circumferinței, proiecția acesteia (umbra în raze paralele de lumină) face o mișcare oscilatorie armonică pe un ecran vertical (Fig. 13.2).
Deplasarea de la poziția de echilibru în timpul vibrațiilor armonice este descrisă de o ecuație (se numește legea cinematică a mișcării armonice) de forma:
\(x = A \cos \Bigr(\frac(2 \pi)(T)t + \varphi_0 \Bigl)\) sau \(x = A \sin \Bigr(\frac(2 \pi)(T) t + \varphi"_0 \Bigl)\)
Unde X- amestecare - o valoare care caracterizeaza pozitia punctului oscilant in momentul de timp t relativ la poziția de echilibru și măsurată prin distanța de la poziția de echilibru la poziția punctului la un moment dat în timp; A- amplitudinea oscilatiei - deplasarea maxima a corpului din pozitia de echilibru; T- perioada de oscilatie - timpul unei oscilatii complete; acestea. cea mai mică perioadă de timp după care se repetă valorile mărimilor fizice care caracterizează oscilația; \(\varphi_0\) - faza inițială; \(\varphi = \frac(2 \pi)(T)t + \varphi"_0\) - faza de oscilație în timp t. Faza de oscilație este un argument al unei funcții periodice, care, pentru o amplitudine de oscilație dată, determină în orice moment starea sistemului oscilator (deplasare, viteză, accelerație) a corpului.
Daca la momentul initial t0 = 0 punctul oscilant este deplasat maxim de la poziția de echilibru, apoi \(\varphi_0 = 0\), iar deplasarea punctului din poziția de echilibru se modifică conform legii
\(x = A \cos \frac(2 \pi)(T)t.\)
Dacă punctul de oscilație la t 0 = 0 se află într-o poziție de echilibru stabil, atunci deplasarea punctului din poziția de echilibru se modifică conform legii
\(x = A \sin \frac(2 \pi)(T)t.\)
valoarea V, reciproca perioadei și egală cu numărul de oscilații complete efectuate în 1 s, se numește frecventa de oscilatie:
\(\nu = \frac(1)(T) \)(în SI unitatea de frecvență este hertz, 1Hz = 1s -1).
Dacă la timp t organismul se angajează Nîn plină desfășurare, atunci
\(T = \frac(t)(N) ; \nu = \frac(N)(t).\)
Valoarea \(\omega = 2 \pi \nu = \frac(2 \pi)(T)\), care arată câte oscilații face corpul în 2 \(\pi\) Cu, numit frecvență ciclică (circulară).
Legea cinematică a mișcării armonice poate fi scrisă astfel:
\(x = A \cos(2\pi \nu t + \varphi_0), x = A \cos(\omega t + \varphi_0).\)
Grafic, dependența deplasării unui punct oscilant în timp este reprezentată de un cosinus (sau sinusoid).
Figura 13.3, a prezintă dependența de timp a deplasării punctului oscilant față de poziția de echilibru pentru cazul \(\varphi_0=0\), adică. \(~x=A\cos \omega t.\)
Să aflăm cum se modifică viteza unui punct oscilant în timp. Pentru a face acest lucru, găsim derivata în timp a acestei expresii:
\(\upsilon_x = x" A \sin \omega t = \omega A \cos \Bigr(\omega t + \frac(\pi)(2) \Bigl) ,\)
unde \(~\omega A = |\upsilon_x|_m\) este amplitudinea proiecției vitezei pe axă X.
Această formulă arată că, în timpul oscilațiilor armonice, proiecția vitezei corpului pe axa x se modifică, de asemenea, conform legii armonice cu aceeași frecvență, cu o amplitudine diferită și este înaintea fazei de amestecare cu \(\frac(\pi). )(2)\) (Fig. 13.3 , b).
Pentru a afla dependența accelerației a x (t) găsiți derivata în timp a proiecției vitezei:
\(~ a_x = \upsilon_x" = -\omega^2 A \cos \omega t = \omega^2 \cos(\omega t + \pi),\)
unde \(~\omega^2 A = |a_x|_m\) este amplitudinea proiecției accelerației pe axă X.
Pentru vibrațiile armonice, proiecția accelerareînaintea defazajului cu k (Fig. 13.3, c).
În mod similar, puteți reprezenta grafic \(~x(t), \upsilon_x (t)\) și \(~a_x(t),\) dacă \(~x = A \sin \omega t\) cu \(\varphi_0 =0.\)
Avand in vedere ca \(A \cos \omega t = x\), se poate scrie formula acceleratiei
\(~a_x = - \omega^2 x,\)
acestea. pentru oscilațiile armonice, proiecția accelerației este direct proporțională cu deplasarea și opusă în semn, i.e. accelerația este îndreptată în direcția opusă deplasării.
Deci, proiecția accelerației este derivata a doua a deplasării și x \u003d x "", atunci raportul rezultat poate fi scris ca:
\(~a_x + \omega^2 x = 0\) sau \(~x"" + \omega^2 x = 0.\)
Se numește ultima egalitate ecuația oscilațiilor armonice.
Un sistem fizic în care pot exista oscilații armonice se numește oscilator armonic,și ecuația oscilațiilor armonice - ecuația oscilatorului armonic.
Literatură
Aksenovich L. A. Fizica în liceu: Teorie. Sarcini. Teste: Proc. indemnizație pentru instituțiile care oferă general. medii, educație / L. A. Aksenovich, N. N. Rakina, K. S. Farino; Ed. K. S. Farino. - Mn.: Adukatsia i vykhavanne, 2004. - S. 368-370.
Modificările unei mărimi sunt descrise folosind legile sinusului sau cosinusului, apoi astfel de oscilații se numesc armonice. Luați în considerare un circuit format dintr-un condensator (care a fost încărcat înainte de a fi inclus în circuit) și un inductor (Fig. 1).
Poza 1.
Ecuația de oscilație armonică poate fi scrisă după cum urmează:
$q=q_0cos((\omega )_0t+(\alpha )_0)$ (1)
unde $t$-timp; $q$ taxă, $q_0$-- abaterea maximă a taxei de la valoarea medie (zero) în timpul modificărilor; $(\omega )_0t+(\alpha )_0$- faza de oscilatie; $(\alpha )_0$ - faza inițială; $(\omega )_0$ - frecvență ciclică. În timpul perioadei, faza se modifică cu $2\pi $.
Tip ecuație:
ecuația oscilațiilor armonice în formă diferențială pentru un circuit oscilator care nu va conține rezistență activă.
Orice fel de oscilații periodice pot fi reprezentate cu acuratețe ca sumă a oscilațiilor armonice, așa-numita serie armonică.
Pentru perioada de oscilație a unui circuit care constă dintr-o bobină și un condensator, obținem formula Thomson:
Dacă diferențiem expresia (1) în funcție de timp, putem obține formula pentru funcția $I(t)$:
Tensiunea pe condensator poate fi găsită ca:
Din formulele (5) și (6) rezultă că puterea curentului este înaintea tensiunii de pe condensator cu $\frac(\pi )(2).$
Oscilațiile armonice pot fi reprezentate atât sub formă de ecuații, funcții și diagrame vectoriale.
Ecuația (1) reprezintă oscilații libere neamortizate.
Ecuația de oscilație amortizată
Modificarea sarcinii ($q$) pe plăcile condensatoarelor din circuit, ținând cont de rezistența (Fig. 2), va fi descrisă printr-o ecuație diferențială de forma:

Figura 2.
Dacă rezistența care face parte din circuitul $R \
unde $\omega =\sqrt(\frac(1)(LC)-\frac(R^2)(4L^2))$ este frecvența de oscilație ciclică. $\beta =\frac(R)(2L)-$factor de atenuare. Amplitudinea oscilațiilor amortizate este exprimată astfel:
În cazul în care la $t=0$ sarcina condensatorului este egală cu $q=q_0$, nu există curent în circuit, atunci pentru $A_0$ putem scrie:
Faza de oscilație în momentul inițial de timp ($(\alpha )_0$) este egală cu:
Pentru $R >2\sqrt(\frac(L)(C))$ modificarea sarcinii nu este o oscilație, descărcarea condensatorului se numește aperiodic.
Exemplul 1
Exercițiu: Valoarea maximă a taxei este $q_0=10\ C$. Se modifică armonic cu perioada $T= 5 c$. Determinați curentul maxim posibil.
Soluţie:
Ca bază pentru rezolvarea problemei, folosim:
Pentru a găsi puterea curentului, expresia (1.1) trebuie diferențiată în funcție de timp:
unde maxima (valoarea amplitudinii) a intensității curentului este expresia:
Din condițiile problemei, cunoaștem valoarea amplitudinii sarcinii ($q_0=10\ Kl$). Ar trebui să găsiți frecvența naturală a oscilațiilor. Să o exprimăm astfel:
\[(\omega )_0=\frac(2\pi )(T)\left(1.4\right).\]
În acest caz, valoarea dorită va fi găsită folosind ecuațiile (1.3) și (1.2) ca:
Deoarece toate mărimile din condițiile problemei sunt prezentate în sistemul SI, vom efectua calculele:
Răspuns:$I_0=12,56\ A.$
Exemplul 2
Exercițiu: Care este perioada de oscilație într-un circuit care conține un inductor $L=1$H și un condensator, dacă curentul din circuit se modifică conform legii: $I\left(t\right)=-0.1sin20\pi t \ \left(A \right)?$ Care este capacitatea condensatorului?
Soluţie:
Din ecuația oscilațiilor curente, care este dată în condițiile problemei:
vedem că $(\omega )_0=20\pi $, prin urmare putem calcula perioada de oscilație folosind formula:
\ \
Conform formulei lui Thomson pentru un circuit care conține un inductor și un condensator, avem:
Să calculăm capacitatea:
Răspuns:$T=0,1$ c, $C=2,5\cdot (10)^(-4)F.$