Curbe de ordinul doi pe un plan sunt drepte definite prin ecuații în care coordonatele variabilei XȘi y sunt cuprinse în gradul doi. Acestea includ elipsa, hiperbola și parabola.
Forma generală a ecuației curbei de ordinul doi este următoarea:
Unde A, B, C, D, E, F- numere și cel puțin unul dintre coeficienți A, B, C nu este egal cu zero.
La rezolvarea problemelor cu curbe de ordinul doi, cel mai adesea sunt luate în considerare ecuațiile canonice ale elipsei, hiperbolei și parabolei. Este ușor să treceți la ele din ecuațiile generale; exemplul 1 de probleme cu elipse îi va fi dedicat.
Elipsa dată de ecuația canonică
Definiţia an elipse. O elipsă este mulțimea tuturor punctelor planului pentru care suma distanțelor până la punctele numite focare este o valoare constantă mai mare decât distanța dintre focare.
Focalizările sunt indicate ca în figura de mai jos.
Ecuația canonică a unei elipse are forma:
Unde AȘi b (A > b) - lungimile semi-axelor, adică jumătate din lungimile segmentelor tăiate de elipsă pe axele de coordonate.
Linia dreaptă care trece prin focarele elipsei este axa ei de simetrie. O altă axă de simetrie a unei elipse este o linie dreaptă care trece prin mijlocul unui segment perpendicular pe acest segment. Punct DESPRE intersecția acestor drepte servește ca centru de simetrie al elipsei sau pur și simplu ca centru al elipsei.
Axa absciselor elipsei se intersectează în punctele ( A, DESPRE) Și (- A, DESPRE), iar axa ordonatelor este în puncte ( b, DESPRE) Și (- b, DESPRE). Aceste patru puncte sunt numite vârfuri ale elipsei. Segmentul dintre vârfurile elipsei de pe axa x se numește axa sa majoră, iar pe axa ordonatelor - axa sa minoră. Segmentele lor dinspre vârf spre centrul elipsei se numesc semi-axe.
Dacă A = b, atunci ecuația elipsei ia forma . Aceasta este ecuația unui cerc cu rază A, iar cercul este caz special elipsă. O elipsă poate fi obținută dintr-un cerc cu rază A, dacă îl comprimați în A/b ori de-a lungul axei Oi .
Exemplul 1. Verificați dacă o dreaptă dată de o ecuație generală este 
, elipsa.
Soluţie. Facem transformări ecuație generală. Folosim transferul termenului liber în partea dreaptă, împărțirea termen cu termen a ecuației cu același număr și reducerea fracțiilor:
Răspuns. Ecuația obținută în urma transformărilor este ecuația canonică a elipsei. Prin urmare, această linie este o elipsă.
Exemplul 2. Compuneți ecuația canonică a unei elipse dacă semiaxele sale sunt 5 și, respectiv, 4.
Soluţie. Ne uităm la formula pentru ecuația canonică a unei elipse și înlocuim: semiaxa majoră este A= 5, semiaxa minoră este b= 4 . Obținem ecuația canonică a elipsei:
Punctele și , indicate cu verde pe axa majoră, unde
sunt numite trucuri.
numit excentricitate elipsă.
Atitudine b/A caracterizează „oblatirea” elipsei. Cu cât acest raport este mai mic, cu atât elipsa este mai alungită de-a lungul axei majore. Cu toate acestea, gradul de alungire al unei elipse este exprimat mai des prin excentricitate, a cărei formulă este dată mai sus. Pentru diferite elipse, excentricitatea variază de la 0 la 1, rămânând întotdeauna mai mică decât unitate.
Exemplul 3. Compuneți ecuația canonică a elipsei dacă distanța dintre focare este 8 și axa majoră este 10.
Soluţie. Să tragem câteva concluzii simple:
Dacă axa majoră este egală cu 10, atunci jumătatea ei, adică semiaxa A = 5 ,
Dacă distanța dintre focare este 8, atunci numărul c dintre coordonatele focale este egală cu 4.
Inlocuim si calculam:
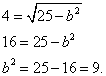
Rezultatul este ecuația canonică a elipsei:
Exemplul 4. Compuneți ecuația canonică a unei elipse dacă axa ei majoră este 26 și excentricitatea ei este .
Soluţie. După cum rezultă atât din dimensiunea axei majore, cât și din ecuația excentricității, semiaxa majoră a elipsei A= 13. Din ecuația excentricității exprimăm numărul c, necesar pentru a calcula lungimea semiaxei minore:
.
Calculăm pătratul lungimii semiaxei minore:
Compunem ecuația canonică a elipsei:
Exemplul 5. Determinați focarele elipsei date de ecuația canonică.
Soluţie. Găsiți numărul c, care determină primele coordonate ale focarelor elipsei:
.
Obținem focusurile elipsei:
Exemplul 6. Focarele elipsei sunt situate pe axă Bou simetric fata de origine. Compuneți ecuația canonică a elipsei dacă:
1) distanța dintre focusuri este 30, iar axa majoră este 34
2) axa minoră 24, iar unul dintre focusuri este în punctul (-5; 0)
3) excentricitate, iar unul dintre focare este în punctul (6; 0)
Să continuăm să rezolvăm împreună problemele elipselor
Dacă este un punct arbitrar al elipsei (indicat cu verde în partea dreaptă sus a elipsei din desen) și este distanța până la acest punct de la focare, atunci formulele pentru distanțe sunt următoarele:
Pentru fiecare punct aparținând elipsei, suma distanțelor de la focare este o valoare constantă egală cu 2 A.
Liniile definite prin ecuații
sunt numite directoare elipsă (în desen există linii roșii de-a lungul marginilor).
Din cele două ecuații de mai sus rezultă că pentru orice punct al elipsei
,
unde si sunt distantele acestui punct fata de directrice si .
Exemplul 7. Dată o elipsă. Scrieți o ecuație pentru directricele sale.
Soluţie. Ne uităm la ecuația directricei și aflăm că trebuie să găsim excentricitatea elipsei, i.e. Avem toate datele pentru asta. Noi calculăm:
.
Obținem ecuația directricelor elipsei:
Exemplul 8. Compuneți ecuația canonică a unei elipse dacă focarele sale sunt puncte și directricele sunt drepte.
Prelegeri de algebră și geometrie. Semestrul 1.
Cursul 15. Elipsa.
Capitolul 15. Elipsa.
clauza 1. Definiții de bază.
Definiție. O elipsă este GMT-ul unui plan, suma distanțelor până la două puncte fixe ale planului, numite focare, este o valoare constantă.
Definiție. Distanța de la un punct arbitrar M al planului până la focarul elipsei se numește raza focală a punctului M.
Denumiri: 
– focarele elipsei, 
– razele focale ale punctului M.
După definiția unei elipse, un punct M este un punct al unei elipse dacă și numai dacă 
– valoare constantă. Această constantă este de obicei notată ca 2a:
.
(1)
observa asta 
.
Prin definiția unei elipse, focarele sale sunt puncte fixe, deci distanța dintre ele este, de asemenea, o valoare constantă pentru o elipsă dată.
Definiție. Distanța dintre focarele elipsei se numește distanță focală.
Desemnare: 
.
Dintr-un triunghi 
urmează că 
, adică
.
Să notăm cu b numărul egal cu 
, adică
.
(2)
Definiție. Atitudine
(3)
se numește excentricitatea elipsei.
Să introducem un sistem de coordonate pe acest plan, pe care îl vom numi canonic pentru elipsă.
Definiție. Axa pe care se află focarele elipsei se numește axă focală.
Să construim un PDSC canonic pentru elipsă, vezi Fig. 2.
Selectăm axa focală ca axa absciselor și trasăm axa ordonatelor prin mijlocul segmentului 
perpendicular pe axa focală.
Apoi focarele au coordonate 
,
.
clauza 2. Ecuația canonică a unei elipse.
Teorema. În sistemul de coordonate canonic pentru o elipsă, ecuația elipsei are forma:
.
(4)
Dovada. Efectuăm dovada în două etape. În prima etapă, vom demonstra că coordonatele oricărui punct situat pe elipsă satisfac ecuația (4). În a doua etapă vom demonstra că orice soluție a ecuației (4) dă coordonatele unui punct situat pe elipsă. De aici rezultă că ecuația (4) este satisfăcută de acele și numai acele puncte ale planului de coordonate care se află pe elipsă. Din aceasta și din definiția ecuației unei curbe va rezulta că ecuația (4) este o ecuație a unei elipse.
1) Fie punctul M(x, y) un punct al elipsei, i.e. suma razelor sale focale este 2a:
.
Să folosim formula pentru distanța dintre două puncte de pe planul de coordonate și să folosim această formulă pentru a găsi razele focale ale unui punct dat M:
,
, de unde obținem:
Să mutăm o rădăcină în partea dreaptă a egalității și să o pătram:
Reducand obtinem:
Vă prezentăm altele asemănătoare, reduceți cu 4 și îndepărtați radicalul:
.
Pătrare
Deschideți parantezele și scurtați 
:
unde ajungem:
Folosind egalitatea (2), obținem:
.
Împărțind ultima egalitate la 
, obținem egalitatea (4), etc.
2) Fie acum o pereche de numere (x, y) satisface ecuația (4) și fie M(x, y) punctul corespunzător pe planul de coordonate Oxy.
Apoi din (4) rezultă:
.
Inlocuim aceasta egalitate in expresia pentru razele focale ale punctului M:
.
Aici am folosit egalitatea (2) și (3).
Prin urmare, 
. De asemenea, 
.
Acum rețineți că din egalitatea (4) rezultă că
sau 
etc. 
, atunci inegalitatea urmează:
.
De aici rezultă, la rândul său, că
sau 
Și
,
.
(5)
Din egalităţi (5) rezultă că 
, adică punctul M(x, y) este un punct al elipsei etc.
Teorema a fost demonstrată.
Definiție. Ecuația (4) se numește ecuația canonică a elipsei.
Definiție. Axele de coordonate canonice ale unei elipse sunt numite axele principale ale elipsei.
Definiție. Originea sistemului de coordonate canonice pentru o elipsă se numește centrul elipsei.
clauza 3. Proprietățile elipsei.
Teorema. (Proprietățile unei elipse.)
1. În sistemul de coordonate canonic pentru o elipsă, totul
punctele elipsei sunt în dreptunghi
,
.
2. Punctele se află
3. O elipsă este o curbă care este simetrică în raport cu
axele lor principale.
4. Centrul elipsei este centrul ei de simetrie.
Dovada. 1, 2) Urmează imediat din ecuația canonică a elipsei.
3, 4) Fie M(x, y) un punct arbitrar al elipsei. Atunci coordonatele sale satisfac ecuația (4). Dar atunci coordonatele punctelor satisfac și ecuația (4) și, prin urmare, sunt puncte ale elipsei, din care urmează enunțurile teoremei.
Teorema a fost demonstrată.
Definiție. Mărimea 2a se numește axa majoră a elipsei, mărimea a se numește semiaxa majoră a elipsei.
Definiție. Mărimea 2b se numește axa mică a elipsei, mărimea b se numește semiaxa mică a elipsei.
Definiție. Punctele de intersecție ale unei elipse cu axele sale principale sunt numite vârfuri ale elipsei.
Cometariu. O elipsă poate fi construită după cum urmează. În avion, „locăm un cui în punctele focale” și fixăm o lungime a firului de ele 
. Apoi luăm un creion și îl folosim pentru a întinde firul. Apoi mutam mina de creion de-a lungul planului, asigurându-ne că firul este întins.
Din definiţia excentricităţii rezultă că
Să fixăm numărul a și să direcționăm numărul c la zero. Apoi la 
,
Și 
. În limita pe care o ajungem
sau 
– ecuația unui cerc.
Să ne direcționăm acum 
. Apoi 
,
si vedem ca in limita elipsa degenereaza intr-un segment de dreapta 
în notația din figura 3.
clauza 4. Ecuații parametrice ale elipsei.
Teorema. Lăsa 
– arbitrar numere reale. Apoi sistemul de ecuații
,
(6)
sunt ecuații parametrice ale unei elipse în sistemul de coordonate canonic pentru elipsă.
Dovada. Este suficient să se demonstreze că sistemul de ecuații (6) este echivalent cu ecuația (4), adică. au același set de soluții.
1) Fie (x, y) o soluție arbitrară a sistemului (6). Împărțiți prima ecuație cu a, a doua cu b, pătrați ambele ecuații și adăugați:
.
Acestea. orice soluție (x, y) a sistemului (6) satisface ecuația (4).
2) Dimpotrivă, fie perechea (x, y) o soluție a ecuației (4), adică.
.
Din această egalitate rezultă că punctul cu coordonate 
se află pe un cerc cu raza unitară cu centrul la origine, adică este un punct dintr-un cerc trigonometric căruia îi corespunde un anumit unghi 
:
Din definiția sinusului și cosinusului rezultă imediat că
,
, Unde 
, din care rezultă că perechea (x, y) este o soluție a sistemului (6), etc.
Teorema a fost demonstrată.
Cometariu. O elipsă poate fi obținută ca urmare a „compresiei” uniforme a unui cerc cu raza a spre axa absciselor.
Lăsa 
– ecuația unui cerc cu centrul la origine. „Comprimarea” unui cerc la axa absciselor nu este altceva decât o transformare a planului de coordonate, efectuată conform următoarei reguli. Pentru fiecare punct M(x, y) asociem un punct pe acelasi plan 
, Unde 
,
- rata compresiei.
Cu această transformare, fiecare punct de pe cerc „tranziție” la un alt punct din plan, care are aceeași abscisă, dar o ordonată mai mică. Să exprimăm vechea ordonată a unui punct prin cea nouă:
și înlocuiți cercuri în ecuație:
.
De aici obținem:
.
(7)
De aici rezultă că dacă înainte de transformarea „compresiei” punctul M(x, y) se afla pe cerc, i.e. coordonatele sale au satisfăcut ecuația cercului, apoi după transformarea „compresiei” acest punct s-a „transformat” în punct 
, ale cărui coordonate satisfac ecuația elipsei (7). Dacă vrem să obținem ecuația unei elipse cu axa semiminorăb, atunci trebuie să luăm factorul de compresie
.
clauza 5. Tangent la o elipsă.
Teorema. Lăsa 
– punctul arbitrar al elipsei
.
Apoi ecuația tangentei la această elipsă în punctul 
are forma:
.
(8)
Dovada. Este suficient să luăm în considerare cazul când punctul de tangență se află în primul sau al doilea sfert al planului de coordonate: 
. Ecuația elipsei din semiplanul superior are forma:
.
(9)
Să folosim ecuația tangentă la graficul funcției 
la punct 
:
Unde 
– valoarea derivatei unei funcții date într-un punct 
. Elipsa din primul trimestru poate fi considerată ca un grafic al funcției (8). Să găsim derivata și valoarea ei în punctul de tangență:
,
. Aici am profitat de faptul că punctul tangent 
este un punct al elipsei și, prin urmare, coordonatele sale satisfac ecuația elipsei (9), adică.
.
Inlocuim valoarea gasita a derivatei in ecuatia tangentei (10):
,
unde ajungem:
Asta implică:
Să împărțim această egalitate la 
:
.
Rămâne de notat că 
, deoarece punct 
aparține elipsei și coordonatele acesteia îi satisfac ecuația.
Ecuația tangentei (8) este demonstrată în mod similar în punctul de tangență situat în al treilea sau al patrulea sfert al planului de coordonate.
Și în cele din urmă, putem verifica cu ușurință că ecuația (8) dă ecuația tangentei în puncte 
,
:
sau 
, Și 
sau 
.
Teorema a fost demonstrată.
clauza 6. Proprietatea oglindă a unei elipse.
Teorema. Tangenta la elipsa are unghiuri egale cu razele focale ale punctului de tangenta.
Lăsa 
- punct de contact, 
,
– razele focale ale punctului tangent, P și Q – proiecțiile focarelor pe tangentele trasate la elipsă în punct 
.
Teorema afirmă că
.
(11)
Această egalitate poate fi interpretată ca egalitatea unghiurilor de incidență și de reflexie a unei raze de lumină dintr-o elipsă eliberată din focalizarea acesteia. Această proprietate se numește proprietatea oglindă a elipsei:
O rază de lumină eliberată din focarul elipsei, după reflectarea din oglinda elipsei, trece printr-un alt focar al elipsei.
Demonstrarea teoremei. Pentru a demonstra egalitatea unghiurilor (11), demonstrăm asemănarea triunghiurilor 
Și 
, în care părțile 
Și 
va fi asemănător. Deoarece triunghiurile sunt dreptunghiulare, este suficient să se demonstreze egalitatea
Linii de ordinul doi.
Elipsa și ecuația ei canonică. Cerc
După un studiu amănunțit linii drepte în plan Continuăm să studiem geometria lumii bidimensionale. Miza este dublată și vă invit să vizitați o pitorească galerie de elipse, hiperbole, parabole, care sunt reprezentanți tipici. linii de ordinul doi. Excursia a început deja și mai întâi o scurtă informare despre întreaga expoziție de la diferite etaje ale muzeului:
Conceptul de dreptă algebrică și ordinea acesteia
O linie pe un plan se numește algebric, dacă în sistem de coordonate afine ecuația sa are forma , unde este un polinom format din termeni de forma ( – număr real, – numere întregi nenegative).
După cum puteți vedea, ecuația unei linii algebrice nu conține sinusuri, cosinusuri, logaritmi și alte frumoase monde funcționale. Doar X și Y sunt în numere întregi nenegative grade.
Ordine de linie egală cu valoarea maximă a termenilor cuprinsi în acesta.
Conform teoremei corespunzătoare, conceptul de dreptă algebrică, precum și ordinea acesteia, nu depind de alegere sistem de coordonate afine, prin urmare, pentru ușurința existenței, presupunem că toate calculele ulterioare au loc în coordonate carteziene.
Ecuație generală a doua linie de ordine are forma , unde 
– numere reale arbitrare (Se obișnuiește să-l scrieți cu un factor de doi), iar coeficienții nu sunt egali cu zero în același timp.
Dacă , atunci ecuația se simplifică la 
, iar dacă coeficienții nu sunt egali cu zero în același timp, atunci acesta este exact ecuația generală a unei linii „plate”., care reprezintă prima linie de comandă.
Mulți au înțeles sensul noilor termeni, dar, cu toate acestea, pentru a stăpâni 100% materialul, băgăm degetele în priză. Pentru a determina ordinea liniilor, trebuie să repetați toți termenii ecuațiile sale și găsiți pentru fiecare dintre ele suma de grade variabilele de intrare.
De exemplu:
termenul conține „x” la puterea 1;
termenul conține „Y” la puterea 1;
Nu există variabile în termen, deci suma puterilor lor este zero.
Acum să ne dăm seama de ce ecuația definește linia al doilea Ordin:
termenul conține „x” la a 2-a putere;
sumandul are suma puterilor variabilelor: 1 + 1 = 2;
termenul conține „Y” la a 2-a putere;
toți ceilalți termeni - Mai puțin grade.
Valoarea maximă: 2
Dacă adăugăm în plus, să zicem, la ecuația noastră, atunci aceasta va determina deja linie de ordinul trei. Este evident că forma generală a ecuației liniei de ordinul 3 conține un „set complet” de termeni, suma puterilor variabilelor în care este egală cu trei:
, unde coeficienții nu sunt egali cu zero în același timp.
În cazul în care adăugați unul sau mai mulți termeni potriviți care conțin 
, atunci vom vorbi deja despre linii de ordinul 4, etc.
Va trebui să întâlnim linii algebrice de ordinul al 3-lea, al 4-lea și superior de mai multe ori, în special atunci când ne familiarizăm cu sistemul de coordonate polare.
Cu toate acestea, să revenim la ecuația generală și să ne amintim cele mai simple variații școlare ale acesteia. Ca exemplu, se sugerează o parabolă, a cărei ecuație poate fi ușor redusă la aspectul general, și o hiperbolă cu ecuația echivalentă . Totuși, nu totul este atât de simplu...
Un dezavantaj semnificativ al ecuației generale este că aproape întotdeauna nu este clar ce linie definește. Chiar și în cel mai simplu caz, nu îți vei da seama imediat că aceasta este o hiperbolă. Astfel de amenajări sunt bune numai la o mascarada, așa că în cursul geometriei analitice luăm în considerare sarcină tipică aducând ecuația liniei de ordinul 2 la forma canonică.
Care este forma canonică a unei ecuații?
Acest lucru este în general acceptat vedere standard ecuație, când în câteva secunde devine clar ce obiect geometric definește. În plus, forma canonică este foarte convenabilă pentru rezolvarea multor probleme practice. Deci, de exemplu, conform ecuației canonice „plat” drept, în primul rând, este imediat clar că aceasta este o linie dreaptă, iar în al doilea rând, punctul care îi aparține și vectorul de direcție sunt ușor vizibile.
Este evident că oricare Prima linie de comandă este o linie dreaptă. La etajul doi, nu ne mai așteaptă paznicul, ci o companie mult mai diversă de nouă statui:
Clasificarea liniilor de ordinul doi
Folosind un set special de acțiuni, orice ecuație a unei linii de ordinul doi este redusă la una dintre următoarele forme:
(și sunt numere reale pozitive)
1) 
– ecuația canonică a elipsei;
2) – ecuația canonică a unei hiperbole;
3) 
– ecuația canonică a unei parabole;
4) – imaginar elipsă;
5) – o pereche de drepte care se intersectează;
6) – pereche imaginar linii de intersectare (cu un singur punct de intersecție valid la origine);
7) – o pereche de drepte paralele;
8) – pereche imaginar linii paralele;
9) – o pereche de linii coincidente.
Unii cititori pot avea impresia că lista este incompletă. De exemplu, la punctul nr. 7, ecuația specifică perechea direct, paralel cu axa, și se pune întrebarea: unde este ecuația care determină dreptele paralele cu axa ordonatelor? Raspunde neconsiderat canonic. Liniile drepte reprezintă același caz standard, rotit cu 90 de grade, iar intrarea suplimentară în clasificare este redundantă, deoarece nu aduce nimic fundamental nou.
Astfel, sunt nouă și doar nouă tipuri variate linii de ordinul 2, dar în practică se găsesc cel mai des elipsa, hiperbola si parabola.
Să ne uităm mai întâi la elipsă. Ca de obicei, mă concentrez pe acele puncte care au mare importanță pentru a rezolva probleme, iar dacă aveți nevoie de o derivare detaliată a formulelor, demonstrații de teoreme, vă rugăm să consultați, de exemplu, manualul lui Bazylev/Atanasyan sau Aleksandrov.
Elipsa și ecuația ei canonică
Ortografie... vă rugăm să nu repetați greșelile unor utilizatori Yandex care sunt interesați de „cum să construiți o elipsă”, „diferența dintre o elipsă și un oval” și „excentricitatea unei elipse”.
Ecuația canonică a unei elipse are forma , unde sunt numere reale pozitive și . Voi formula însăși definiția unei elipse mai târziu, dar deocamdată este timpul să luăm o pauză de la magazinul vorbitor și să rezolvăm o problemă comună:
Cum se construiește o elipsă?
Da, ia-l și desenează-l. Sarcina are loc frecvent și o parte semnificativă a elevilor nu fac față desenului corect:
Exemplul 1
Construiți elipsa dată de ecuație
Soluţie: În primul rând, să aducem ecuația la forma canonică: 
De ce să aduci? Unul dintre avantajele ecuației canonice este că vă permite să determinați instantaneu vârfurile elipsei, care sunt situate în puncte. Este ușor de observat că coordonatele fiecăruia dintre aceste puncte satisfac ecuația.
ÎN în acest caz, :
Segment de linie numit axa majoră elipsă;
segment de linie – axa minoră;
număr 
numit arbore semi-major elipsă;
număr 
– axa minoră.
în exemplul nostru: .
Pentru a vă imagina rapid cum arată o anumită elipsă, priviți doar valorile „a” și „fi” ale ecuației sale canonice.
Totul este bine, neted și frumos, dar există o avertizare: am făcut desenul folosind programul. Și puteți face desenul folosind orice aplicație. Cu toate acestea, în realitate dură, există o bucată de hârtie în carouri pe masă, iar șoarecii dansează în cercuri pe mâinile noastre. Oamenii cu talent artistic, desigur, se pot certa, dar ai și șoareci (deși mai mici). Nu degeaba omenirea a inventat rigla, busola, raportorul și alte dispozitive simple pentru desen.
Din acest motiv, este puțin probabil să reușim să desenăm cu precizie o elipsă cunoscând doar vârfurile. Este în regulă dacă elipsa este mică, de exemplu, cu semi-axe. Alternativ, puteți reduce scara și, în consecință, dimensiunile desenului. Dar, în general, este foarte de dorit să găsiți puncte suplimentare.
Există două abordări pentru construirea unei elipse - geometrică și algebrică. Nu îmi place construcția folosind o busolă și o riglă, deoarece algoritmul nu este cel mai scurt și desenul este semnificativ aglomerat. În caz de urgență, vă rugăm să consultați manualul, dar în realitate este mult mai rațional să folosiți instrumentele algebrei. Din ecuația elipsei din schiță exprimăm rapid: 
Ecuația se descompune apoi în două funcții: 
– definește arcul superior al elipsei; 
– definește arcul inferior al elipsei.
Elipsa definită de ecuația canonică este simetrică față de axele de coordonate, precum și față de origine. Și acest lucru este grozav - simetria este aproape întotdeauna un prevestitor al gratuităților. Evident, este suficient să ne ocupăm de primul trimestru de coordonate, așa că avem nevoie de funcție 
. Se roagă să se găsească puncte suplimentare cu abscise 
. Să atingem trei mesaje SMS pe calculator: 
Desigur, este, de asemenea, frumos că, dacă se face o greșeală gravă în calcule, aceasta va deveni imediat clară în timpul construcției.
Să marchem puncte în desen (roșu), puncte simetrice pe arcele rămase ( Culoarea albastră) și conectați cu atenție întreaga companie cu o linie: 
Este mai bine să desenați schița inițială foarte subțire și abia apoi să aplicați presiune cu un creion. Rezultatul ar trebui să fie o elipsă destul de decentă. Apropo, ai vrea să știi ce este această curbă?
Definiţia an elipse. Focare de elipsă și excentricitate de elipsă
O elipsă este un caz special al unui oval. Cuvântul „oval” nu trebuie înțeles în sensul filistin („copilul a desenat un oval”, etc.). Acesta este un termen matematic care are o formulare detaliată. Scopul acestei lecții nu este de a lua în considerare teoria ovalelor și diferitele lor tipuri, cărora practic nu li se acordă atenție în cursul standard de geometrie analitică. Și, în conformitate cu nevoile mai actuale, trecem imediat la definiția strictă a unei elipse:
Elipsă este mulțimea tuturor punctelor planului, suma distanțelor până la fiecare dintre ele de la două puncte date, numite trucuri elipsa, este o mărime constantă, numeric egală cu lungimea axei majore a acestei elipse: .
În același timp, distanțele dintre focus sunt mai mici valoare dată: .
Acum totul va deveni mai clar: 
Imaginează-ți că punctul albastru „călătorește” de-a lungul unei elipse. Deci, indiferent de ce punct al elipsei luăm, suma lungimilor segmentelor va fi întotdeauna aceeași:
Să ne asigurăm că în exemplul nostru valoarea sumei este într-adevăr egală cu opt. Puneți mental punctul „um” la vârful din dreapta al elipsei, apoi: , care este ceea ce trebuia verificat.
O altă metodă de desenare se bazează pe definiția unei elipse. Matematica superioară este uneori cauza tensiunii și a stresului, așa că este timpul să avem o altă sesiune de descărcare. Vă rog să luați ce hârtie sau frunză mare carton și bate-l pe masă cu două cuie. Acestea vor fi trucuri. Legați un fir verde de capetele proeminente ale unghiilor și trageți-l până la capăt cu un creion. Mina de creion va ajunge la un anumit punct care aparține elipsei. Acum începeți să mutați creionul de-a lungul bucății de hârtie, păstrând firul verde întins. Continuati procesul pana reveniti la punctul de plecare... super... desenul poate fi verificat de medic si profesor =)
Cum să găsiți focarele unei elipse?
În exemplul de mai sus, am descris punctele focale „gata făcute”, iar acum vom învăța cum să le extragem din adâncurile geometriei.
Dacă o elipsă este dată de o ecuație canonică, atunci focarele sale au coordonate 
, unde este distanța de la fiecare focar până la centrul de simetrie al elipsei.
Calculele sunt mai simple decât simple: 
! Coordonatele specifice ale focarelor nu pot fi identificate cu semnificația „tse”! Repet că asta este DISTANTA de la fiecare focalizare la centru(care în cazul general nu trebuie să fie situat exact la origine).
Și, prin urmare, distanța dintre focare, de asemenea, nu poate fi legată de poziția canonică a elipsei. Cu alte cuvinte, elipsa poate fi mutată în alt loc, iar valoarea va rămâne neschimbată, în timp ce focarele își vor schimba în mod natural coordonatele. Vă rugăm să luați în considerare acest lucru pe măsură ce explorați în continuare subiectul.
Excentricitatea elipsei și semnificația ei geometrică
Excentricitatea unei elipse este un raport care poate lua valori în intervalul .
În cazul nostru:
Să aflăm cum forma unei elipse depinde de excentricitatea acesteia. Pentru aceasta fixați vârfurile stânga și dreapta a elipsei luate în considerare, adică valoarea semiaxei majore va rămâne constantă. Atunci formula excentricității va lua forma: .
Să începem să aducem valoarea excentricității mai aproape de unitate. Acest lucru este posibil numai dacă . Ce înseamnă? ... ține minte trucurile 
. Aceasta înseamnă că focarele elipsei se vor „depărta” de-a lungul axei absciselor până la vârfurile laterale. Și, deoarece „segmentele verzi nu sunt din cauciuc”, elipsa va începe inevitabil să se aplatizeze, transformându-se într-un cârnați din ce în ce mai subțiri înșirat pe o axă.
Prin urmare, cu cât valoarea excentricității elipsei este mai aproape de unitate, cu atât elipsa este mai alungită.
Acum să modelăm procesul opus: focarele elipsei 
mers unul spre celălalt, apropiindu-se de centru. Aceasta înseamnă că valoarea lui „ce” devine din ce în ce mai mică și, în consecință, excentricitatea tinde spre zero: .
În acest caz, „segmentele verzi” vor „deveni aglomerate”, dimpotrivă, și vor începe să „împingă” linia elipsei în sus și în jos.
Prin urmare, Cu cât valoarea excentricității este mai aproape de zero, cu atât elipsa este mai asemănătoare... uitați-vă la cazul limitativ când focarele sunt reunite cu succes la origine:
Un cerc este un caz special al unei elipse
Într-adevăr, în cazul egalității semiaxelor, ecuația canonică a elipsei ia forma , care se transformă reflexiv în ecuația unui cerc cu un centru la originea razei „a”, binecunoscută din școală.
În practică, se folosește mai des notația cu litera „vorbitoare” „er”: . Raza este lungimea unui segment, fiecare punct al cercului îndepărtat de centru cu o distanță de rază.
Rețineți că definiția unei elipse rămâne complet corectă: focarele coincid, iar suma lungimilor segmentelor coincidente pentru fiecare punct de pe cerc este o constantă. Deoarece distanța dintre focare este , atunci excentricitatea oricărui cerc este zero.
Construirea unui cerc este ușoară și rapidă, doar folosește o busolă. Cu toate acestea, uneori este necesar să aflăm coordonatele unora dintre punctele sale, în acest caz mergem pe calea familiară - aducem ecuația la forma vesela Matanov:
– funcția semicercului superior;
– funcţia semicercului inferior.
După care găsim valorile cerute, diferențiați, integrași să faci alte lucruri bune.
Articolul, desigur, este doar pentru referință, dar cum poți trăi în lume fără iubire? Sarcina creativă pentru decizie independentă
Exemplul 2
Compuneți ecuația canonică a unei elipse dacă unul dintre focarele și semiaxa ei sunt cunoscute (centrul este la origine). Găsiți vârfuri, puncte suplimentare și trageți o linie în desen. Calculați excentricitatea.
Rezolvare și desen la sfârșitul lecției
Să adăugăm o acțiune:
Rotiți și translați în paralel o elipsă
Să revenim la ecuația canonică a elipsei, și anume la condiția, al cărei mister chinuiește minți curios de la prima menţiune a acestei curbe. Așa că ne-am uitat la elipsă 
, dar nu este posibil în practică să îndeplinim ecuația 
? La urma urmei, aici, însă, pare a fi și o elipsă!
Acest tip de ecuație este rar, dar se întâlnește. Și definește de fapt o elipsă. Să demitificăm: 
În urma construcției s-a obținut elipsa noastră nativă, rotită cu 90 de grade. Acesta este, 
- Acest intrare necanonică elipsă 
. Record!- ecuația 
nu definește nicio altă elipsă, deoarece nu există puncte (focare) pe axă care să satisfacă definiția unei elipse.
O elipsă este locul geometric al punctelor dintr-un plan, suma distanțelor de la fiecare dintre acestea la două puncte date F_1, iar F_2 este o valoare constantă (2a), mai mare decât distanța (2c) dintre aceste puncte date (Fig. 3.36, a). Această definiție geometrică exprimă proprietatea focală a unei elipse.
Proprietatea focală a unei elipse
Punctele F_1 și F_2 sunt numite focare ale elipsei, distanța dintre ele 2c=F_1F_2 este distanța focală, mijlocul O al segmentului F_1F_2 este centrul elipsei, numărul 2a este lungimea axei majore a elipsei. elipsa (în consecință, numărul a este semi-axa majoră a elipsei). Segmentele F_1M și F_2M care leagă un punct arbitrar M al elipsei cu focarele sale se numesc raze focale ale punctului M. Segmentul care leagă două puncte ale unei elipse se numește coardă a elipsei.
Raportul e=\frac(c)(a) se numește excentricitatea elipsei. Din definiția (2a>2c) rezultă că 0\leqslant e<1 . При e=0 , т.е. при c=0 , фокусы F_1 и F_2 , а также центр O совпадают, и эллипс является окружностью радиуса a (рис.3.36,6).
Definiția geometrică a elipsei, exprimându-și proprietatea focală, este echivalentă cu definiția sa analitică - linia dată de ecuația canonică a elipsei:
Într-adevăr, să introducem un sistem de coordonate dreptunghiular (Fig. 3.36c). Luăm centrul O al elipsei ca origine a sistemului de coordonate; luăm drept axa care trece prin focare (axa focală sau prima axă a elipsei) drept axă de abscisă (direcția pozitivă pe aceasta este de la punctul F_1 la punctul F_2); să luăm o dreaptă perpendiculară pe axa focală și care trece prin centrul elipsei (a doua axă a elipsei) ca axa ordonatelor (direcția pe axa ordonatelor este aleasă astfel încât sistem dreptunghiular coordonatele Oxy s-a dovedit a avea dreptate).
Să creăm o ecuație pentru elipsă folosind definiția sa geometrică, care exprimă proprietatea focală. În sistemul de coordonate selectat, determinăm coordonatele focarelor F_1(-c,0),~F_2(c,0). Pentru un punct arbitrar M(x,y) aparținând elipsei, avem:
\vline\,\overrightarrow(F_1M)\,\vline\,+\vline\,\overrightarrow(F_2M)\,\vline\,=2a.
Scriind această egalitate sub formă de coordonate, obținem:
\sqrt((x+c)^2+y^2)+\sqrt((x-c)^2+y^2)=2a.
Mutăm al doilea radical în partea dreaptă, pătram ambele părți ale ecuației și aducem termeni similari:
(x+c)^2+y^2=4a^2-4a\sqrt((x-c)^2+y^2)+(x-c)^2+y^2~\Leftrightarrow ~4a\sqrt((x-c) )^2+y^2)=4a^2-4cx.
Împărțind la 4, pătratăm ambele părți ale ecuației:
A^2(x-c)^2+a^2y^2=a^4-2a^2cx+c^2x^2~\Leftrightarrow~ (a^2-c^2)^2x^2+a^2y^ 2=a^2(a^2-c^2).
După ce a desemnat b=\sqrt(a^2-c^2)>0, primim b^2x^2+a^2y^2=a^2b^2. Împărțind ambele părți la a^2b^2\ne0, ajungem la ecuația canonică a elipsei:
\frac(x^2)(a^2)+\frac(y^2)(b^2)=1.
Prin urmare, sistemul de coordonate ales este canonic.
Dacă focarele elipsei coincid, atunci elipsa este un cerc (Fig. 3.36,6), deoarece a=b. În acest caz, orice sistem de coordonate dreptunghiular cu originea în punct va fi canonic O\equiv F_1\equiv F_2, iar ecuația x^2+y^2=a^2 este ecuația unui cerc cu centrul în punctul O și raza egală cu a.
Prin rationamentul in ordine inversă, se poate arăta că toate punctele ale căror coordonate satisfac ecuația (3.49), și numai ele, aparțin locului geometric al punctelor numit elipsă. Cu alte cuvinte, definiția analitică a unei elipse este echivalentă cu a acesteia definiție geometrică, exprimând proprietatea focală a unei elipse.
Proprietatea directorială a unei elipse
Directricele unei elipse sunt două linii drepte paralele cu axa ordonatelor sistemului de coordonate canonic la aceeași distanță \frac(a^2)(c) de acesta. La c=0, când elipsa este un cerc, nu există directrice (putem presupune că directricele sunt la infinit).
Elipsa cu excentricitate 0
De fapt, de exemplu, pentru focus F_2 și directrix d_2 (Fig. 3.37,6) condiția \frac(r_2)(\rho_2)=e poate fi scris sub formă de coordonate:
\sqrt((x-c)^2+y^2)=e\cdot\!\left(\frac(a^2)(c)-x\right)
A scăpa de iraționalitate și a înlocui e=\frac(c)(a),~a^2-c^2=b^2, ajungem la ecuația canonică a elipsei (3.49). Raționament similar poate fi efectuat pentru focus F_1 și director d_1\colon\frac(r_1)(\rho_1)=e.
Ecuația unei elipse într-un sistem de coordonate polare
Ecuația elipsei în sistemul de coordonate polar F_1r\varphi (Fig. 3.37, c și 3.37 (2)) are forma
R=\frac(p)(1-e\cdot\cos\varphi)
unde p=\frac(b^2)(a) este parametrul focal al elipsei.
De fapt, să alegem focarul din stânga F_1 al elipsei ca pol al sistemului de coordonate polare și raza F_1F_2 ca axă polară (Fig. 3.37, c). Atunci pentru un punct arbitrar M(r,\varphi), conform definiției geometrice (proprietatea focală) a unei elipse, avem r+MF_2=2a. Exprimăm distanța dintre punctele M(r,\varphi) și F_2(2c,0) (vezi paragraful 2 din observațiile 2.8):
\begin(aligned)F_2M&=\sqrt((2c)^2+r^2-2\cdot(2c)\cdot r\cos(\varphi-0))=\\ &=\sqrt(r^2- 4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2).\end(aligned)
Prin urmare, sub formă de coordonate, ecuația elipsei F_1M+F_2M=2a are forma
R+\sqrt(r^2-4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2)=2\cdot a.
Izolăm radicalul, pătram ambele părți ale ecuației, împărțim la 4 și prezentăm termeni similari:
R^2-4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2~\Leftrightarrow~a\cdot\!\left(1-\frac(c)(a)\cdot\cos \varphi\right)\!\cdot r=a^2-c^2.
Exprimați raza polară r și faceți înlocuirea e=\frac(c)(a),~b^2=a^2-c^2,~p=\frac(b^2)(a):
R=\frac(a^2-c^2)(a\cdot(1-e\cdot\cos\varphi)) \quad \Leftrightarrow \quad r=\frac(b^2)(a\cdot(1) -e\cdot\cos\varphi)) \quad \Leftrightarrow \quad r=\frac(p)(1-e\cdot\cos\varphi),
Q.E.D.
Semnificația geometrică a coeficienților din ecuația elipsei
Să găsim punctele de intersecție ale elipsei (vezi Fig. 3.37a) cu axele de coordonate (vârfurile elipsei). Substituind y=0 în ecuație, găsim punctele de intersecție ale elipsei cu axa absciselor (cu axa focală): x=\pm a. Prin urmare, lungimea segmentului axei focale conținut în interiorul elipsei este egală cu 2a. Acest segment, după cum s-a menționat mai sus, este numit axa majoră a elipsei, iar numărul a este semiaxa majoră a elipsei. Înlocuind x=0, obținem y=\pm b. Prin urmare, lungimea segmentului celei de-a doua axe a elipsei conținut în interiorul elipsei este egală cu 2b. Acest segment se numește axa minoră a elipsei, iar numărul b este semiaxa minoră a elipsei.
Într-adevăr, b=\sqrt(a^2-c^2)\leqslant\sqrt(a^2)=a, iar egalitatea b=a se obține numai în cazul c=0, când elipsa este un cerc. Atitudine k=\frac(b)(a)\leqslant1 se numește raportul de compresie al elipsei.
Note 3.9
1. Dreptele x=\pm a,~y=\pm b limitează dreptunghiul principal pe planul de coordonate, în interiorul căruia se află o elipsă (vezi Fig. 3.37, a).
2. O elipsă poate fi definită ca locul punctelor obţinute prin comprimarea unui cerc până la diametrul acestuia.
Într-adevăr, fie ecuația unui cerc în sistemul de coordonate dreptunghiular Oxy x^2+y^2=a^2. Când este comprimat pe axa x cu un coeficient de 0 \begin(cases)x"=x,\\y"=k\cdot y.\end(cases) Înlocuind cercurile x=x" și y=\frac(1)(k)y" în ecuație, obținem ecuația pentru coordonatele imaginii M"(x",y") ale punctului M(x,y ) : (x")^2+(\left(\frac(1)(k)\cdot y"\right)\^2=a^2 \quad \Leftrightarrow \quad \frac{(x")^2}{a^2}+\frac{(y")^2}{k^2\cdot a^2}=1 \quad \Leftrightarrow \quad \frac{(x")^2}{a^2}+\frac{(y")^2}{b^2}=1,
!} întrucât b=k\cdot a . Aceasta este ecuația canonică a elipsei. 3. Axele de coordonate (ale sistemului de coordonate canonic) sunt axele de simetrie ale elipsei (numite axele principale ale elipsei), iar centrul acesteia este centrul de simetrie. Într-adevăr, dacă punctul M(x,y) aparține elipsei . atunci punctele M"(x,-y) și M""(-x,y), simetrice față de punctul M față de axele de coordonate, aparțin și ele aceleiași elipse. 4. Din ecuația elipsei din sistemul de coordonate polare r=\frac(p)(1-e\cos\varphi)(vezi Fig. 3.37, c), semnificația geometrică a parametrului focal este clarificat - aceasta este jumătate din lungimea coardei elipsei care trece prin focarul său perpendicular pe axa focală ( r = p la \varphi=\frac(\pi)(2)). 5. Excentricitatea e caracterizează forma elipsei și anume diferența dintre elipsă și cerc. Cu cât e mai mare, cu atât elipsa este mai alungită și cu cât e mai aproape de zero, cu atât elipsa este mai aproape de un cerc (Fig. 3.38a). Într-adevăr, ținând cont că e=\frac(c)(a) și c^2=a^2-b^2 , obținem E^2=\frac(c^2)(a^2)=\frac(a^2-b^2)(a^2)=1-(\left(\frac(a)(b)\right )\^2=1-k^2,
!} unde k este raportul de compresie al elipsei, 0 6. Ecuația \frac(x^2)(a^2)+\frac(y^2)(b^2)=1 la o
7. Ecuația \frac((x-x_0)^2)(a^2)+\frac((y-y_0)^2)(b^2)=1,~a\geqslant b definește o elipsă cu centru în punctul O"(x_0,y_0), ale cărei axe sunt paralele cu axele de coordonate (Fig. 3.38, c). Această ecuație se reduce la cea canonică folosind translația paralelă (3.36). Când a=b=R ecuația (x-x_0)^2+(y-y_0)^2=R^2 descrie un cerc de raza R cu centrul în punctul O"(x_0,y_0) . Ecuația parametrică a elipseiîn sistemul de coordonate canonic are forma \begin(cases)x=a\cdot\cos(t),\\ y=b\cdot\sin(t),\end(cases)0\leqslant t<2\pi.
Într-adevăr, înlocuind aceste expresii în ecuația (3.49), ajungem la identitatea trigonometrică principală \cos^2t+\sin^2t=1 . Exemplul 3.20. Desenați o elipsă \frac(x^2)(2^2)+\frac(y^2)(1^2)=1în sistemul de coordonate canonic Oxy. Găsiți semiaxele, distanța focală, excentricitatea, raportul de compresie, parametrul focal, ecuațiile directrice. Soluţie. Comparând ecuația dată cu cea canonică, determinăm semiaxele: a=2 - semiaxa majoră, b=1 - semiaxa minoră a elipsei. Construim dreptunghiul principal cu laturile 2a=4,~2b=2 cu centrul la origine (Fig. 3.39). Având în vedere simetria elipsei, o potrivim în dreptunghiul principal. Dacă este necesar, determinați coordonatele unor puncte ale elipsei. De exemplu, înlocuind x=1 în ecuația elipsei, obținem \frac(1^2)(2^2)+\frac(y^2)(1^2)=1 \quad \Leftrightarrow \quad y^2=\frac(3)(4) \quad \Leftrightarrow \ quad y=\pm\frac(\sqrt(3))(2). Prin urmare, puncte cu coordonate \left(1;\,\frac(\sqrt(3))(2)\right)\!,~\left(1;\,-\frac(\sqrt(3))(2)\right)- aparțin elipsei. Calcularea raportului de compresie k=\frac(b)(a)=\frac(1)(2); distanta focala 2c=2\sqrt(a^2-b^2)=2\sqrt(2^2-1^2)=2\sqrt(3); excentricitate e=\frac(c)(a)=\frac(\sqrt(3))(2); parametru focal p=\frac(b^2)(a)=\frac(1^2)(2)=\frac(1)(2). Compunem ecuațiile directrice: x=\pm\frac(a^2)(c)~\Leftrightarrow~x=\pm\frac(4)(\sqrt(3)).Ecuația parametrică a elipsei
Pentru a efectua calcule, trebuie să activați controalele ActiveX!
