Among all the diversity logarithmic inequalities Inequalities with variable bases are studied separately. They are solved using a special formula, which for some reason is rarely taught in school:
log k (x) f (x) ∨ log k (x) g (x) ⇒ (f (x) − g (x)) (k (x) − 1) ∨ 0
Instead of the “∨” checkbox, you can put any inequality sign: more or less. The main thing is that in both inequalities the signs are the same.
This way we get rid of logarithms and reduce the problem to rational inequality. The latter is much easier to solve, but when discarding logarithms, extra roots may appear. To cut them off, it is enough to find the range of acceptable values. If you have forgotten the ODZ of a logarithm, I strongly recommend repeating it - see “What is a logarithm”.
Everything related to the range of acceptable values must be written out and solved separately:
f(x) > 0; g(x) > 0; k(x) > 0; k(x) ≠ 1.
These four inequalities constitute a system and must be satisfied simultaneously. When the range of acceptable values has been found, all that remains is to intersect it with the solution of the rational inequality - and the answer is ready.
Task. Solve the inequality:
First, let’s write out the logarithm’s ODZ:
The first two inequalities are satisfied automatically, but the last one will have to be written out. Since the square of the number equal to zero if and only if the number itself is zero, we have:
x 2 + 1 ≠ 1;
x 2 ≠ 0;
x ≠ 0.
It turns out that the ODZ of the logarithm is all numbers except zero: x ∈ (−∞ 0)∪(0; +∞). Now we solve the main inequality:

We make the transition from logarithmic inequality to rational one. The original inequality has a “less than” sign, which means the resulting inequality must also have a “less than” sign. We have:
(10 − (x 2 + 1)) · (x 2 + 1 − 1)< 0;
(9 − x 2) x 2< 0;
(3 − x ) (3 + x ) x 2< 0.
The zeros of this expression are: x = 3; x = −3; x = 0. Moreover, x = 0 is a root of the second multiplicity, which means that when passing through it, the sign of the function does not change. We have:

We get x ∈ (−∞ −3)∪(3; +∞). This set is completely contained in the ODZ of the logarithm, which means this is the answer.
Converting logarithmic inequalities
Often the original inequality is different from the one above. This can be easily corrected using the standard rules for working with logarithms - see “Basic properties of logarithms”. Namely:
- Any number can be represented as a logarithm with a given base;
- The sum and difference of logarithms with the same bases can be replaced by one logarithm.
Separately, I would like to remind you about the range of acceptable values. Since there may be several logarithms in the original inequality, it is required to find the VA of each of them. Thus, general scheme solutions to logarithmic inequalities are as follows:
- Find the VA of each logarithm included in the inequality;
- Reduce the inequality to a standard one using the formulas for adding and subtracting logarithms;
- Solve the resulting inequality using the scheme given above.
Task. Solve the inequality:
Let's find the domain of definition (DO) of the first logarithm:
We solve using the interval method. Finding the zeros of the numerator:
3x − 2 = 0;
x = 2/3.
Then - the zeros of the denominator:
x − 1 = 0;
x = 1.
We mark zeros and signs on the coordinate arrow:

We get x ∈ (−∞ 2/3)∪(1; +∞). The second logarithm will have the same VA. If you don't believe me, you can check it. Now we transform the second logarithm so that the base is two:
As you can see, the threes at the base and in front of the logarithm have been reduced. We got two logarithms with the same base. Let's add them up:

log 2 (x − 1) 2< 2;
log 2 (x − 1) 2< log 2 2 2 .
We obtained the standard logarithmic inequality. We get rid of logarithms using the formula. Since the original inequality contains a “less than” sign, the resulting rational expression must also be less than zero. We have:
(f (x) − g (x)) (k (x) − 1)< 0;
((x − 1) 2 − 2 2)(2 − 1)< 0;
x 2 − 2x + 1 − 4< 0;
x 2 − 2x − 3< 0;
(x − 3)(x + 1)< 0;
x ∈ (−1; 3).
We got two sets:
- ODZ: x ∈ (−∞ 2/3)∪(1; +∞);
- Candidate answer: x ∈ (−1; 3).
It remains to intersect these sets - we get the real answer:

We are interested in the intersection of sets, so we select intervals that are shaded on both arrows. We get x ∈ (−1; 2/3)∪(1; 3) - all points are punctured.
Definition of logarithm The easiest way to write it mathematically is:
The definition of logarithm can be written in another way:
Pay attention to the restrictions that are imposed on the base of the logarithm ( a) and to the sublogarithmic expression ( x). In the future, these conditions will turn into important restrictions for OD, which will need to be taken into account when solving any equation with logarithms. So, now, in addition to the standard conditions leading to restrictions on ODZ (positivity of expressions under the roots of even powers, non-equal denominator to zero, etc.), the following conditions must also be taken into account:
- Sublogarithmic expression can only be positive.
- The base of the logarithm can only be positive and not equal to one.
Note that neither the base of the logarithm nor the sublogarithmic expression can be equal to zero. Please also note that the logarithm value itself can take on all possible values, i.e. The logarithm can be positive, negative or zero. Logarithms have many different properties that follow from the properties of powers and the definition of a logarithm. Let's list them. So, the properties of logarithms:

Logarithm of the product:
Logarithm of a fraction:

Taking the degree out of the logarithm sign:
Pay especially close attention to those of the last listed properties in which the modulus sign appears after the degree is taken. Do not forget that when placing an even power outside the logarithm sign, under the logarithm or at the base, you must leave the modulus sign.
Other beneficial features logarithms:

![]()
The last property is very often used in complex logarithmic equations and inequalities. He should be remembered as well as everyone else, although he is often forgotten.
The simplest logarithmic equations have the form:
![]()
And their solution is given by a formula that directly follows from the definition of the logarithm:
Other simplest logarithmic equations are those that, using algebraic transformations and the above formulas and properties of logarithms, can be reduced to the form:
The solution to such equations taking into account the ODZ is as follows:
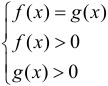
Some others logarithmic equations with a variable at the base can be reduced to the form:
![]()
In such logarithmic equations general form the solution also follows directly from the definition of the logarithm. Only in this case there are additional restrictions for DZ that need to be taken into account. As a result, to solve a logarithmic equation with a variable in the base, you need to solve the following system:

When solving more complex logarithmic equations that cannot be reduced to one of the equations presented above, it is also actively used variable replacement method. As usual, when using this method, you need to remember that after introducing the replacement, the equation should simplify and no longer contain the old unknown. You also need to remember to perform reverse substitution of variables.
Sometimes when solving logarithmic equations you also have to use graphic method. This method consists of constructing graphs of functions that are on the left and right sides of the equation as accurately as possible on one coordinate plane, and then finding the coordinates of their intersection points from the drawing. The roots obtained in this way must be checked by substitution into the original equation.
When solving logarithmic equations it is often also useful grouping method. When using this method, the main thing to remember is that: in order for the product of several factors to be equal to zero, it is necessary that at least one of them is equal to zero, and the rest existed. When the factors are logarithms or parentheses with logarithms, and not just parentheses with variables as in rational equations, many errors can occur. Since logarithms have many restrictions on the region where they exist.
When deciding systems of logarithmic equations most often you have to use either the substitution method or the variable replacement method. If there is such a possibility, then when solving systems of logarithmic equations, one must strive to ensure that each of the equations of the system is individually brought to a form in which it will be possible to make the transition from a logarithmic equation to a rational one.
The simplest logarithmic inequalities are solved in approximately the same way as similar equations. First, using algebraic transformations and the properties of logarithms, we must try to bring them to a form where the logarithms on the left and right sides of the inequality will have the same bases, i.e. get an inequality of the form:
After which you need to move to a rational inequality, taking into account that this transition should be performed as follows: if the base of the logarithm is greater than one, then the sign of the inequality does not need to be changed, and if the base of the logarithm is less than one, then you need to change the sign of the inequality to the opposite (this means changing "less" to "more" or vice versa). In this case, there is no need to change the minus signs to plus ones, bypassing the previously learned rules. Let's write down mathematically what we get as a result of performing such a transition. If the base is greater than one we get:

If the base of the logarithm is less than one, we change the sign of the inequality and get the following system:

As we see, when solving logarithmic inequalities, as usual, the ODZ is also taken into account (this is the third condition in the systems above). Moreover, in this case it is possible not to require the positivity of both sublogarithmic expressions, but rather to require only the positivity of the smaller of them.
When deciding logarithmic inequalities with a variable at the base logarithm, it is necessary to independently consider both options (when the base is less than one and greater than one) and combine the solutions of these cases into a set. At the same time, we must not forget about DL, i.e. about the fact that both the base and all sublogarithmic expressions must be positive. Thus, when solving an inequality of the form:
We obtain the following set of systems:

More complex logarithmic inequalities can also be solved using changes of variables. Some other logarithmic inequalities (like logarithmic equations) require the procedure of taking the logarithm of both sides of the inequality or equation to the same base to solve. So, when carrying out such a procedure with logarithmic inequalities, there is a subtlety. Please note that when taking logarithms to a base greater than one, the inequality sign does not change, but if the base is less than one, then the inequality sign is reversed.
If a logarithmic inequality cannot be reduced to a rational one or solved using a substitution, then in this case one must use generalized interval method, which is as follows:
- Define DL;
- Transform the inequality so that there is a zero on the right side (on the left side, if possible, reduce to a common denominator, factorize, etc.);
- Find all the roots of the numerator and denominator and plot them on the number axis, and if the inequality is not strict, paint over the roots of the numerator, but in any case leave the roots of the denominator as dotted out;
- Find the sign of the entire expression on each of the intervals by substituting a number from a given interval into the transformed inequality. In this case, it is no longer possible to alternate signs in any way when passing through points on the axis. It is necessary to determine the sign of an expression on each interval by substituting the value from the interval into this expression, and so on for each interval. There’s no way else (that’s what it’s all about, by and large, the difference between the generalized interval method and the usual one);
- Find the intersection of the ODZ and intervals that satisfy the inequality, but do not lose individual points that satisfy the inequality (the roots of the numerator in non-strict inequalities), and do not forget to exclude from the answer all the roots of the denominator in all inequalities.
- Back
- Forward
How to successfully prepare for the CT in physics and mathematics?
In order to successfully prepare for the CT in physics and mathematics, among other things, it is necessary to fulfill three most important conditions:
- Study all topics and complete all tests and assignments given in the educational materials on this site. To do this, you need nothing at all, namely: devote three to four hours every day to preparing for the CT in physics and mathematics, studying theory and solving problems. The fact is that the CT is an exam where it is not enough just to know physics or mathematics, you also need to be able to quickly and without failures solve a large number of problems on different topics and of varying complexity. The latter can only be learned by solving thousands of problems.
- Learn all the formulas and laws in physics, and formulas and methods in mathematics. In fact, this is also very simple to do; there are only about 200 necessary formulas in physics, and even a little less in mathematics. Each of these subjects has about a dozen standard methods for solving problems basic level difficulties that can also be learned, and thus, completely automatically and without difficulty, solve most of the CT at the right time. After this, you will only have to think about the most difficult tasks.
- Attend all three stages of rehearsal testing in physics and mathematics. Each RT can be visited twice to decide on both options. Again, on the CT, in addition to the ability to quickly and efficiently solve problems, and knowledge of formulas and methods, you must also be able to properly plan time, distribute forces, and most importantly, correctly fill out the answer form, without confusing the numbers of answers and problems, or your own last name. Also, during RT, it is important to get used to the style of asking questions in problems, which may seem very unusual to an unprepared person at the DT.
Successful, diligent and responsible implementation of these three points will allow you to show up on the CT excellent result, the maximum of what you are capable of.
Found a mistake?
If you think you have found an error in educational materials, then please write about it by email. You can also report a bug to social network(). In the letter, indicate the subject (physics or mathematics), the name or number of the topic or test, the number of the problem, or the place in the text (page) where, in your opinion, there is an error. Also describe what the suspected error is. Your letter will not go unnoticed, the error will either be corrected, or you will be explained why it is not an error.
LOGARITHMIC INEQUALITIES IN THE USE
Sechin Mikhail Alexandrovich
Small Academy of Sciences for Students of the Republic of Kazakhstan “Iskatel”
MBOU "Sovetskaya Secondary School No. 1", 11th grade, town. Sovetsky Sovetsky district
Gunko Lyudmila Dmitrievna, teacher of the Municipal Budgetary Educational Institution “Sovetskaya Secondary School No. 1”
Sovetsky district
Goal of the work: study of the mechanism for solving logarithmic inequalities C3 using non-standard methods, identifying interesting facts logarithm
Subject of study:
3) Learn to solve specific logarithmic inequalities C3 using non-standard methods.
Results:
Content
Introduction………………………………………………………………………………….4
Chapter 1. History of the issue……………………………………………………...5
Chapter 2. Collection of logarithmic inequalities ………………………… 7
2.1. Equivalent transitions and the generalized method of intervals…………… 7
2.2. Rationalization method……………………………………………………………… 15
2.3. Non-standard substitution……………….................................................... ..... 22
2.4. Tasks with traps……………………………………………………27
Conclusion……………………………………………………………………………… 30
Literature……………………………………………………………………. 31
Introduction
I am in 11th grade and plan to enter a university where the core subject is mathematics. That’s why I work a lot with problems in part C. In task C3, I need to solve a non-standard inequality or system of inequalities, usually related to logarithms. When preparing for the exam, I was faced with the problem of a shortage of methods and techniques for solving exam logarithmic inequalities offered in C3. Methods that are studied in school curriculum on this topic, do not provide a basis for solving C3 tasks. The math teacher suggested that I work on C3 assignments independently under her guidance. In addition, I was interested in the question: do we encounter logarithms in our lives?
With this in mind, the topic was chosen:
“Logarithmic inequalities in the Unified State Exam”
Goal of the work: study of the mechanism for solving C3 problems using non-standard methods, identifying interesting facts about the logarithm.
Subject of study:
1) Find the necessary information about non-standard methods solutions to logarithmic inequalities.
2) Find additional information about logarithms.
3) Learn to solve specific C3 problems using non-standard methods.
Results:
The practical significance lies in the expansion of the apparatus for solving C3 problems. This material can be used in some lessons, for clubs, and elective classes in mathematics.
The project product will be the collection “C3 Logarithmic Inequalities with Solutions.”
Chapter 1. Background
Throughout the 16th century, the number of approximate calculations increased rapidly, primarily in astronomy. Improving instruments, studying planetary movements and other work required colossal, sometimes multi-year, calculations. Astronomy was in real danger of drowning in unfulfilled calculations. Difficulties arose in other areas, for example, in the insurance business, compound interest tables were needed to different meanings percent. The main difficulty was multiplication and division of multi-digit numbers, especially trigonometric quantities.
The discovery of logarithms was based on the properties of progressions that were well known by the end of the 16th century. On the connection between the terms of the geometric progression q, q2, q3, ... and arithmetic progression their indicators are 1, 2, 3,... Archimedes spoke in his “Psalmitis”. Another prerequisite was the extension of the concept of degree to negative and fractional exponents. Many authors have pointed out that multiplication, division, exponentiation and root extraction in geometric progression correspond in arithmetic - in the same order - addition, subtraction, multiplication and division.
Here was the idea of the logarithm as an exponent.
In the history of the development of the doctrine of logarithms, several stages have passed.
Stage 1
Logarithms were invented no later than 1594 independently by the Scottish Baron Napier (1550-1617) and ten years later by the Swiss mechanic Bürgi (1552-1632). Both wanted to provide a new, convenient means of arithmetic calculations, although they approached this problem in different ways. Napier kinematically expressed the logarithmic function and thereby entered a new field of function theory. Bürgi remained on the basis of considering discrete progressions. However, the definition of the logarithm for both is not similar to the modern one. The term "logarithm" (logarithmus) belongs to Napier. It arose from a combination of Greek words: logos - “relation” and ariqmo - “number”, which meant “number of relations”. Initially, Napier used a different term: numeri artificiales - “artificial numbers”, as opposed to numeri naturalts - “natural numbers”.
In 1615, in a conversation with Henry Briggs (1561-1631), a professor of mathematics at Gresh College in London, Napier suggested taking zero as the logarithm of one, and 100 as the logarithm of ten, or, what amounts to the same thing, just 1. This is how decimal logarithms and The first logarithmic tables were printed. Later, Briggs' tables were supplemented by the Dutch bookseller and mathematics enthusiast Adrian Flaccus (1600-1667). Napier and Briggs, although they came to logarithms earlier than everyone else, published their tables later than the others - in 1620. The signs log and Log were introduced in 1624 by I. Kepler. The term “natural logarithm” was introduced by Mengoli in 1659 and followed by N. Mercator in 1668, and the London teacher John Speidel published tables of natural logarithms of numbers from 1 to 1000 under the name “New Logarithms”.
The first logarithmic tables were published in Russian in 1703. But in all logarithmic tables there were calculation errors. The first error-free tables were published in 1857 in Berlin, processed by the German mathematician K. Bremiker (1804-1877).
Stage 2
Further development of the theory of logarithms is associated with a wider application of analytical geometry and infinitesimal calculus. By that time, the connection between the quadrature of an equilateral hyperbola and the natural logarithm had been established. The theory of logarithms of this period is associated with the names of a number of mathematicians.
German mathematician, astronomer and engineer Nikolaus Mercator in an essay
"Logarithmotechnics" (1668) gives a series giving the expansion of ln(x+1) in
powers of x:
This expression exactly corresponds to his train of thought, although, of course, he did not use the signs d, ..., but more cumbersome symbolism. With the discovery of the logarithmic series, the technique for calculating logarithms changed: they began to be determined using infinite series. In his lectures" Elementary mathematics With highest point vision", read in 1907-1908, F. Klein proposed using the formula as the starting point for constructing the theory of logarithms.
Stage 3
Definition of a logarithmic function as an inverse function
exponential, logarithm as an exponent of a given base
was not formulated immediately. Essay by Leonhard Euler (1707-1783)
"An Introduction to the Analysis of Infinitesimals" (1748) served to further
development of the theory of logarithmic functions. Thus,
134 years have passed since logarithms were first introduced
(counting from 1614), before mathematicians came to the definition
the concept of logarithm, which is now the basis of the school course.
Chapter 2. Collection of logarithmic inequalities
2.1. Equivalent transitions and the generalized method of intervals.
Equivalent transitions
 , if a > 1
, if a > 1
 , if 0 <
а <
1
, if 0 <
а <
1

Generalized interval method
This method most universal when solving inequalities of almost any type. The solution diagram looks like this:
1. Bring the inequality to the form where the function on the left side is  , and on the right 0.
, and on the right 0.
2. Find the domain of the function  .
.
3. Find the zeros of the function  , that is, solve the equation
, that is, solve the equation  (and solving an equation is usually easier than solving an inequality).
(and solving an equation is usually easier than solving an inequality).
4. Draw the domain of definition and zeros of the function on the number line.
5. Determine the signs of the function  on the obtained intervals.
on the obtained intervals.
6. Select intervals where the function takes the required values and write down the answer.
Example 1.

Solution:

Let's apply the interval method

where
For these values, all expressions under the logarithmic signs are positive.
Answer:
Example 2.
![]()
Solution:
1st way . ADL is determined by inequality x> 3. Taking logarithms for such x to base 10, we get
The last inequality could be solved by applying expansion rules, i.e. comparing the factors to zero. However, in in this case easy to determine intervals of constant sign of a function
therefore, the interval method can be applied.
Function f(x) = 2x(x- 3.5)lgǀ x- 3ǀ is continuous at x> 3 and vanishes at points x 1 = 0, x 2 = 3,5, x 3 = 2, x 4 = 4. Thus, we determine the intervals of constant sign of the function f(x):

Answer:
2nd method . Let us directly apply the ideas of the interval method to the original inequality.
To do this, recall that the expressions a b- a c and ( a - 1)(b- 1) have one sign. Then our inequality at x> 3 is equivalent to inequality
![]()
or
The last inequality is solved using the interval method
Answer:
Example 3.
![]()
Solution:



Let's apply the interval method

Answer:

Example 4.

Solution:
Since 2 x 2 - 3x+ 3 > 0 for all real x, That


To solve the second inequality we use the interval method

In the first inequality we make the replacement

then we come to the inequality 2y 2 - y - 1 < 0 и, применив метод интервалов, получаем, что решениями будут те y, which satisfy the inequality -0.5< y < 1.

![]()
From where, because
we get the inequality

which is carried out when x, for which 2 x 2 - 3x - 5 < 0. Вновь применим метод интервалов

Now, taking into account the solution to the second inequality of the system, we finally obtain

Answer:
Example 5.
![]()
Solution:
Inequality is equivalent to a collection of systems


or

Let's use the interval method or

Answer:

Example 6.
![]()
Solution:
Inequality equals system

Let
Then y > 0,
![]()
and the first inequality
system takes the form
![]()
or, unfolding
quadratic trinomial factored,
![]()
Applying the interval method to the last inequality,

we see that its solutions satisfying the condition y> 0 will be all y > 4.
Thus, the original inequality is equivalent to the system:

So, the solutions to the inequality are all
![]()
2.2. Rationalization method.
Previously, inequality was not solved using the rationalization method; it was not known. This is the "new modern" effective method solutions to exponential and logarithmic inequalities" (quote from the book by S.I. Kolesnikova)
And even if the teacher knew him, there was a fear - does the Unified State Exam expert know him, and why don’t they give him at school? There were situations when the teacher said to the student: “Where did you get it? Sit down - 2.”
Now the method is being promoted everywhere. And for experts there is guidelines, associated with this method, and in the "Most complete editions typical options..." Solution C3 uses this method.
WONDERFUL METHOD!
"Magic Table"

In other sources
If a >1 and b >1, then log a b >0 and (a -1)(b -1)>0;
If a >1 and 0 if 0<a<1 и b
>1, then log a b<0 и (a
-1)(b
-1)<0;
if 0<a<1 и 00 and (a -1)(b -1)>0. The reasoning carried out is simple, but significantly simplifies the solution of logarithmic inequalities. Example 4.
log x (x 2 -3)<0
Solution:
Example 5.
log 2 x (2x 2 -4x +6)≤log 2 x (x 2 +x ) Solution: Example 6.
To solve this inequality, instead of the denominator, we write (x-1-1)(x-1), and instead of the numerator, we write the product (x-1)(x-3-9 + x). Example 7.
Example 8.
2.3. Non-standard substitution. Example 1.
Example 2.
Example 3.
Example 4.
Example 5.
Example 6.
Example 7.
log 4 (3 x -1)log 0.25 Let's make the replacement y=3 x -1; then this inequality will take the form Log 4 log 0.25 Because log 0.25 Let us make the replacement t =log 4 y and obtain the inequality t 2 -2t +≥0, the solution of which is the intervals - Thus, to find the values of y we have a set of two simple inequalities Therefore, the original inequality is equivalent to the set of two exponential inequalities, The solution to the first inequality of this set is the interval 0<х≤1, решением второго – промежуток 2≤х<+ Example 8.
Solution:
Inequality equals system The solution to the second inequality defining the ODZ will be the set of those x,
for which x > 0.
To solve the first inequality we make the substitution Then we get the inequality or The set of solutions to the last inequality is found by the method intervals: -1< t < 2. Откуда, возвращаясь к переменной x, we get or Lots of those x, which satisfy the last inequality belongs to ODZ ( x> 0), therefore, is a solution to the system, and hence the original inequality. Answer: 2.4. Tasks with traps. Example 1.
Solution. The ODZ of the inequality is all x satisfying the condition 0 Example 2.
log 2 (2 x +1-x 2)>log 2 (2 x-1 +1-x)+1.





 Answer. (0; 0.5)U.
Answer. (0; 0.5)U.
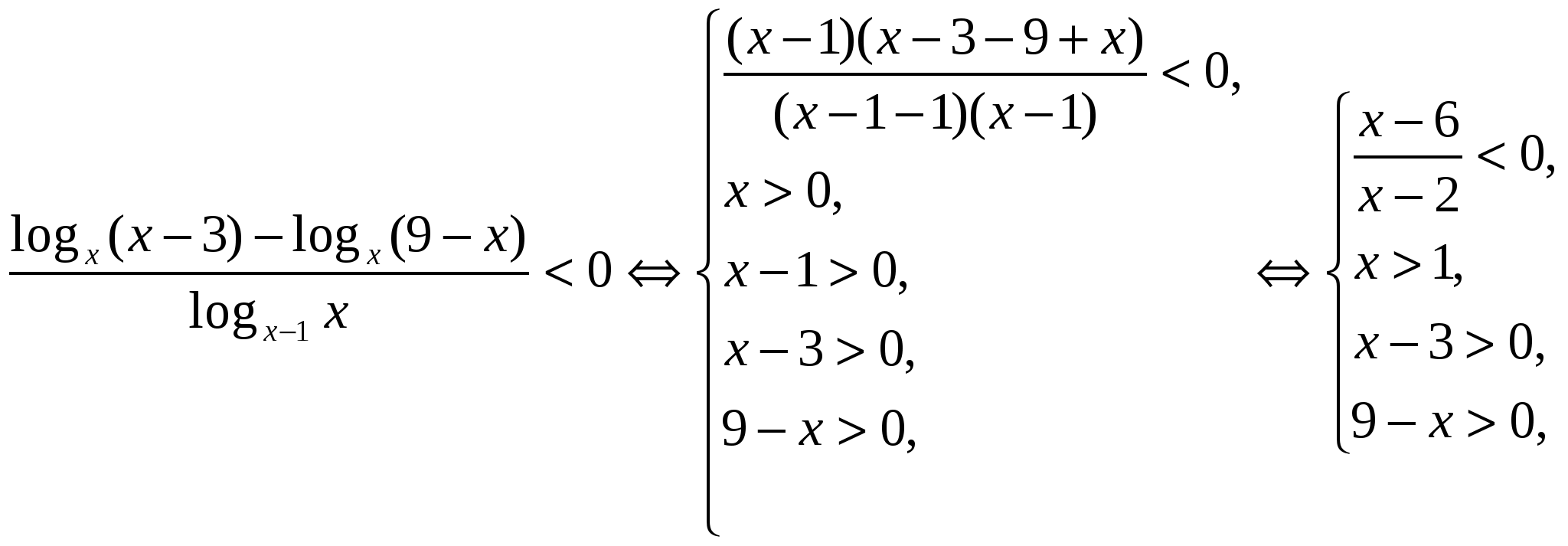

 Answer :
(3;6)
Answer :
(3;6)









 .
.
 = -log 4
= -log 4  = -(log 4 y -log 4 16)=2-log 4 y , then we rewrite the last inequality as 2log 4 y -log 4 2 y ≤.
= -(log 4 y -log 4 16)=2-log 4 y , then we rewrite the last inequality as 2log 4 y -log 4 2 y ≤.
 The solution to this set is the intervals 0<у≤2 и 8≤у<+
The solution to this set is the intervals 0<у≤2 и 8≤у<+ .
.
 that is, aggregates
that is, aggregates 
 . Thus, the original inequality is satisfied for all values of x from the intervals 0<х≤1 и 2≤х<+
. Thus, the original inequality is satisfied for all values of x from the intervals 0<х≤1 и 2≤х<+ .
.


![]()
![]()
![]()


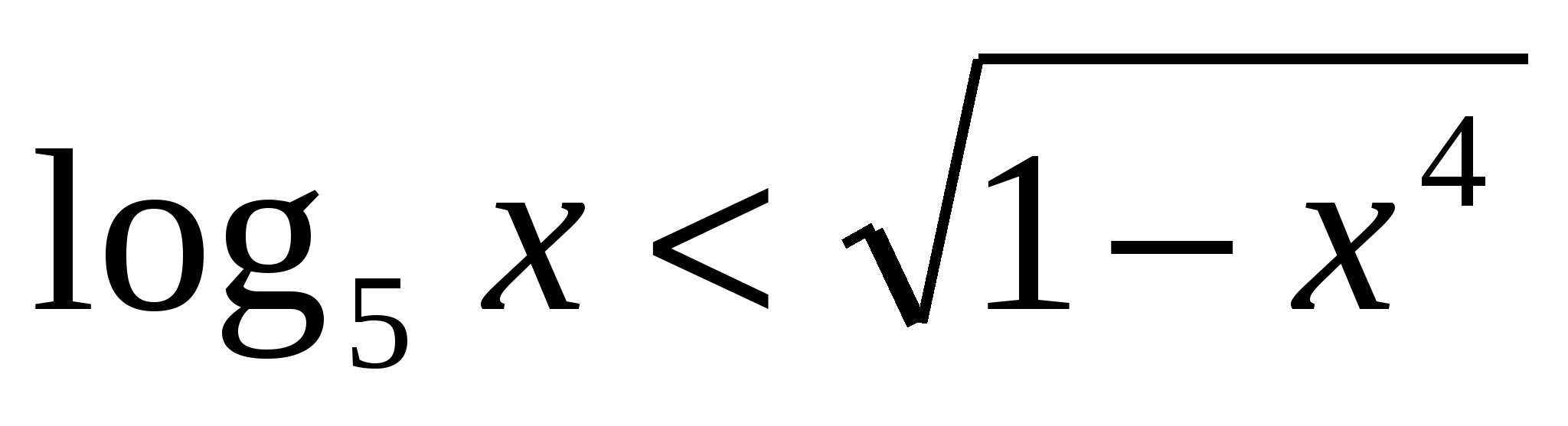 .
.
 . Therefore, all x are from the interval 0
. Therefore, all x are from the interval 0
Conclusion
It was not easy to find specific methods for solving C3 problems from a large abundance of different educational sources. In the course of the work done, I was able to study non-standard methods for solving complex logarithmic inequalities. These are: equivalent transitions and the generalized method of intervals, the method of rationalization , non-standard substitution , tasks with traps on ODZ. These methods are not included in the school curriculum.
Using different methods, I solved 27 inequalities proposed on the Unified State Exam in part C, namely C3. These inequalities with solutions by methods formed the basis of the collection “C3 Logarithmic Inequalities with Solutions,” which became a project product of my activity. The hypothesis I posed at the beginning of the project was confirmed: C3 problems can be effectively solved if you know these methods.
In addition, I discovered interesting facts about logarithms. It was interesting for me to do this. My project products will be useful for both students and teachers.
Conclusions:
Thus, the project goal has been achieved and the problem has been solved. And I received the most complete and varied experience of project activities at all stages of work. While working on the project, my main developmental impact was on mental competence, activities related to logical mental operations, the development of creative competence, personal initiative, responsibility, perseverance, and activity.
A guarantee of success when creating a research project for I gained: significant school experience, the ability to obtain information from various sources, check its reliability, and rank it by importance.
In addition to direct subject knowledge in mathematics, I expanded my practical skills in the field of computer science, gained new knowledge and experience in the field of psychology, established contacts with classmates, and learned to cooperate with adults. During the project activities, organizational, intellectual and communicative general educational skills were developed.
Literature
1. Koryanov A. G., Prokofiev A. A. Systems of inequalities with one variable (standard tasks C3).
2. Malkova A. G. Preparation for the Unified State Exam in Mathematics.
3. Samarova S. S. Solving logarithmic inequalities.
4. Mathematics. Collection of training works edited by A.L. Semenov and I.V. Yashchenko. -M.: MTsNMO, 2009. - 72 p.-
Logarithmic inequalities
In previous lessons, we got acquainted with logarithmic equations and now we know what they are and how to solve them. Today's lesson will be devoted to the study of logarithmic inequalities. What are these inequalities and what is the difference between solving a logarithmic equation and an inequality?
Logarithmic inequalities are inequalities that have a variable appearing under the logarithm sign or at its base.
Or, we can also say that a logarithmic inequality is an inequality in which its unknown value, as in a logarithmic equation, will appear under the sign of the logarithm.
The simplest logarithmic inequalities have the following form:
where f(x) and g(x) are some expressions that depend on x.
Let's look at this using this example: f(x)=1+2x+x2, g(x)=3x−1.
Solving logarithmic inequalities
Before solving logarithmic inequalities, it is worth noting that when solved they are similar to exponential inequalities, namely:
First, when moving from logarithms to expressions under the logarithm sign, we also need to compare the base of the logarithm with one;
Secondly, when solving a logarithmic inequality using a change of variables, we need to solve inequalities with respect to the change until we get the simplest inequality.
But you and I have considered similar aspects of solving logarithmic inequalities. Now let’s pay attention to a rather significant difference. You and I know that the logarithmic function has a limited domain of definition, therefore, when moving from logarithms to expressions under the logarithm sign, we need to take into account the range of permissible values (ADV).
That is, it should be taken into account that when solving a logarithmic equation, you and I can first find the roots of the equation, and then check this solution. But solving a logarithmic inequality will not work this way, since moving from logarithms to expressions under the logarithm sign, it will be necessary to write down the ODZ of the inequality.
In addition, it is worth remembering that the theory of inequalities consists of real numbers, which are positive and negative numbers, as well as the number 0.
For example, when the number “a” is positive, then you need to use the following notation: a >0. In this case, both the sum and the product of these numbers will also be positive.
The main principle for solving an inequality is to replace it with a simpler inequality, but the main thing is that it is equivalent to the given one. Further, we also obtained an inequality and again replaced it with one that has a simpler form, etc.
When solving inequalities with a variable, you need to find all its solutions. If two inequalities have the same variable x, then such inequalities are equivalent, provided that their solutions coincide.
When performing tasks on solving logarithmic inequalities, you must remember that when a > 1, then the logarithmic function increases, and when 0< a < 1, то такая функция имеет свойство убывать. Эти свойства вам будут необходимы при решении логарифмических неравенств, поэтому вы их должны хорошо знать и помнить.
Methods for solving logarithmic inequalities
Now let's look at some of the methods that take place when solving logarithmic inequalities. For better understanding and assimilation, we will try to understand them using specific examples.
We all know that the simplest logarithmic inequality has the following form:
In this inequality, V – is one of the following inequality signs:<,>, ≤ or ≥.
When the base of a given logarithm is greater than one (a>1), making the transition from logarithms to expressions under the logarithm sign, then in this version the inequality sign is preserved, and the inequality will have the following form:
which is equivalent to this system:

In the case when the base of the logarithm is greater than zero and less than one (0 This is equivalent to this system: Let's look at more examples of solving the simplest logarithmic inequalities shown in the picture below: Exercise. Let's try to solve this inequality: Solving the range of acceptable values. Now let's try to multiply its right side by: Let's see what we can come up with: Now, let's move on to converting sublogarithmic expressions. Due to the fact that the base of the logarithm is 0< 1/4 <1, то от сюда следует, что знак неравенства изменится на противоположный: 3x - 8 > 16; And from this it follows that the interval that we obtained entirely belongs to the ODZ and is a solution to such an inequality. Here's the answer we got: Now let's try to analyze what we need to successfully solve logarithmic inequalities? First, concentrate all your attention and try not to make mistakes when performing the transformations that are given in this inequality. Also, it should be remembered that when solving such inequalities, it is necessary to avoid expansions and contractions of the inequalities, which can lead to the loss or acquisition of extraneous solutions. Secondly, when solving logarithmic inequalities, you need to learn to think logically and understand the difference between concepts such as a system of inequalities and a set of inequalities, so that you can easily select solutions to the inequality, while being guided by its DL. Thirdly, to successfully solve such inequalities, each of you must perfectly know all the properties of elementary functions and clearly understand their meaning. Such functions include not only logarithmic, but also rational, power, trigonometric, etc., in a word, all those that you studied during school algebra. As you can see, having studied the topic of logarithmic inequalities, there is nothing difficult in solving these inequalities, provided that you are careful and persistent in achieving your goals. To avoid any problems in solving inequalities, you need to practice as much as possible, solving various tasks and at the same time remember the basic methods of solving such inequalities and their systems. If you fail to solve logarithmic inequalities, you should carefully analyze your mistakes so as not to return to them again in the future. To better understand the topic and consolidate the material covered, solve the following inequalities:

Solving Examples
![]()



3x > 24;
x > 8. ![]()
What is needed to solve logarithmic inequalities?
Homework